はじめに
前回はPythonの機械学習モジュールであるscikit-learnの中にあるクラスタリングのアルゴリズムであるk-meansを使って、irisデータセットをクラスタリングしてみました。irisデータセットですが、種類を含めると5つの列がある5次元データです。このデータをk-meansのアルゴリズムの中に入れて計算処理したのですが、この処理の中身は人間のアタマではイメージすることが難しいものです。つまり「処理がブラックボックス化されていると言えます。
今回はこの多次元データをもう少し人間の感覚的に理解しやすくなる「次元の圧縮」という方法をご紹介したいと思います。今回ご紹介するのは主成分分析(PCA)という手法です。
主成分分析(しゅせいぶんぶんせき、英: principal component analysis; PCA)は、相関のある多数の変数から相関のない少数で全体のばらつきを最もよく表す主成分と呼ばれる変数を合成する多変量解析の一手法。データの次元を削減するために用いられる。
出典: フリー百科事典『ウィキペディア(Wikipedia)』
さて、この中にある「データの次元を削減する」というのはどんなことなのでしょうか?
主成分分析(PCA)による「次元の圧縮」ってなんだ?
この引用の意味を理解するには大学レベル程度の数学(線形代数および統計学)の知識が必要になるので、数学的な厳密性は考えないこととして、直感的な理解を得ようとするにとどめます。
元のデータセットの分散をできる限り残すように次元削減することは、高次元のデータセットを可視化する上で重要である。例えば、主成分の数を L = 2 に選び、2つの主成分がなす平面にデータセットを射影すると、射影されたデータ点は主成分のなす平面に対して最もよく分散し、データに含まれるクラスタはそれぞれ分離される。
出典: フリー百科事典『ウィキペディア(Wikipedia)』
やや乱暴な説明ですが、例えば、「身長、体重、血糖値、年齢、、」というデータが有ったとして、次元を圧縮する場合「身長、体重」→「BMI」、「血糖値、年齢」→「糖尿病予備群」のようにデータから抽象化します。これを数学的に線形代数および統計学を使って表現すると、
主成分は観測値のセットの直交基底となっている。主成分ベクトルの直交性は、主成分ベクトルが共分散行列(あるいは相関行列)の固有ベクトルになっており、共分散行列が実対称行列であることから導かれる。(以下省略)
出典: フリー百科事典『ウィキペディア(Wikipedia)』
なのですが、この表現を数学的な説明無しに理解するのは大変なので、
多くの場合、多変量データは次元が大きく、各変数を軸にとって視覚化することは難しいが、主成分分析によって情報をより少ない次元に集約することでデータを視覚化できる。
出典: フリー百科事典『ウィキペディア(Wikipedia)』
という引用をご紹介するにとどめて先を急ぎたいと思います。
scikit-learnの主成分分析(PCA)を使って次元の圧縮をする処理の流れ
それでは処理の流れを説明します!
scikit-learnの主成分分析(PCA)をインポートし、irisデータを学習
scikit-learnの主成分分析(PCA)をインポートしたら、あらかじめロードしておいたirisのデータフレームを学習させましょう。
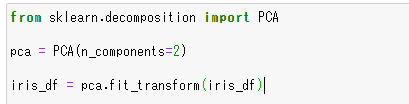
前段のながながとした説明の割には3行で終わりです笑。
pca = PCA(n_components=2)
PCAの引数であるn_componentsで2を指定し、2次元に圧縮するようにしています。
主成分分析で次元の圧縮をした結果を散布図で表現する
matplotlibを使って散布図を表現してみます。

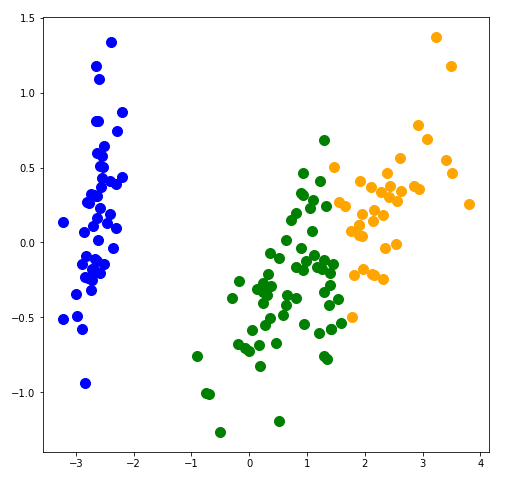
実行結果です。次元を圧縮したため、従来のデータよりきれいに分類されています。
次元の圧縮前のデータと見比べてみる
次元の圧縮前のデータを多次元で散布図表現してみたものと比較してみましょう。まずは圧縮前の4次元データをすべて散布図表現したものです。
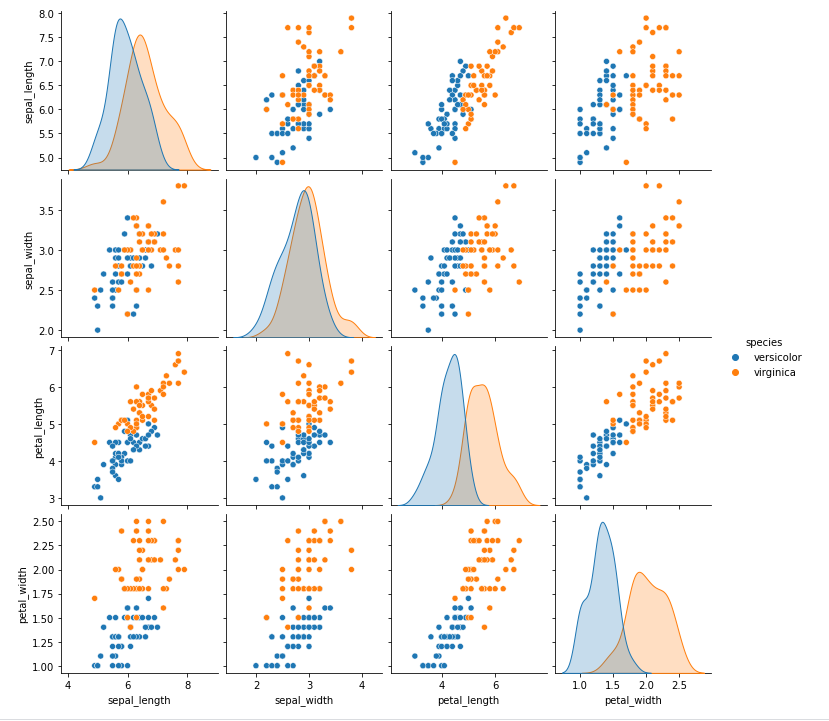
そして、今回圧縮したデータです。データの特徴がはっきりした形となりました。
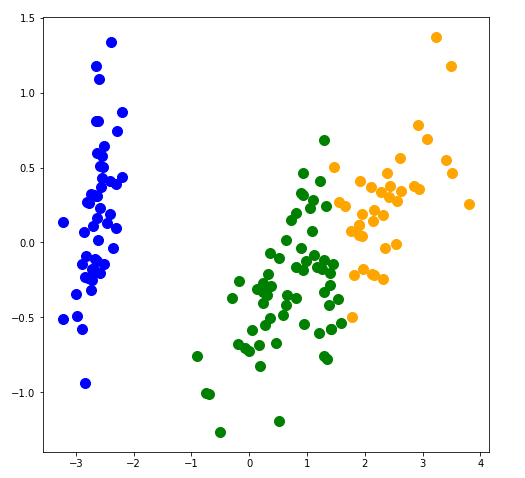
scikit-learnの主成分分析(PCA)を使って次元の圧縮をするサンプルコード
それではサンプルコードです!
from sklearn.decomposition import PCA pca = PCA(n_components=2) iris_df = pca.fit_transform(iris_df) plt.figure(figsize=(8,8)) colors = ['green', 'blue', 'orange'] for i in range(clusters): plt.scatter(iris_df[y_pred==i][:,0], iris_df[y_pred==i][:,1], s=100, c=colors[i]) plt.show()
おわりに
本記事ではscikit-learnの主成分分析(PCA)をインポートし、irisデータの次元を圧縮してみました。主成分分析(PCA)は数学的に難しいですが、その意味するところを理解しておけば、とても強力な分析ツールになります。
データの特徴をはっきり掴むことで、分析を見通すことができるようになるでしょう。