はじめに
前回の記事ではscikit-learnのiris(あやめ)のデータを使ってロジスティクス回帰による分類問題に挑戦しました。使用したデータは、比較的素直な分類しやすいデータだったので、ロジィステック回帰でも適度な分類ができたと思います。
しかし、実際のデータはそう簡単に分類できないものも多くあります。特にデータの中で潜在的に分割できるポイントがあればいいのですが、実際はそうとは限りません。考えてみれば当然で、ぱっと見でデータに相関関係が見て取れる場合、そのデータを分析に回すことはないでしょう。
本記事ではこうしたカンタンに分類できないデータ(線形分類不能なデータを)分類する方法として、scikit-learnの分類アルゴリズムであるサポートベクターマシン(SVM)をご紹介します。本格的にSVMを理解しようとすると大学院レベルの数学が必要となりますので、あまり内部のメカニズムには立ち入らずにその使い方と驚くべき性能についてご紹介したいと思います。
※本記事の内容を実機で試してみたいという方は以下の記事を参考に開発環境をご準備ください
・Pythonやるならド定番!Anacondaをサクッと入れて巨人の肩に乗りましょう!
・Win10&Anaconda3環境でJupyter Notebookを起動してプログラムを実行する方法
・個人情報保護方針及び免責事項
線形分類不能なデータでサポートベクターマシンを使う目的
それではサポートベクターマシンについて概要を把握しておきましょう!
サポートベクターマシンってどんなアルゴリズム?
サポートベクターマシン(英: support vector machine, SVM)は、教師あり学習を用いるパターン認識モデルの一つである。分類や回帰へ適用できる。
サポートベクターマシン wipipediaより
サポートベクターマシーンは教師あり学習を用いるパターン認識アルゴリズムの一つです。数学的に高度なモデルで、大学院生博士課程くらいの人たちでないと数理モデルに関して十分な理解を得ることは難しいでしょう。以下のような数式の羅列を読みこなす自身がある方はトライしてみてください。

サポートベクターマシンを使うのはどんなときか?
線形回帰不可のデータを扱うときにサポートベクターマシンを使用します。線形回帰不能とは、データを分類するときに境界線を引くのが困難なときです。例えば、前回ご紹介したirisのデータは線形分類しやすい素直なデータでした。
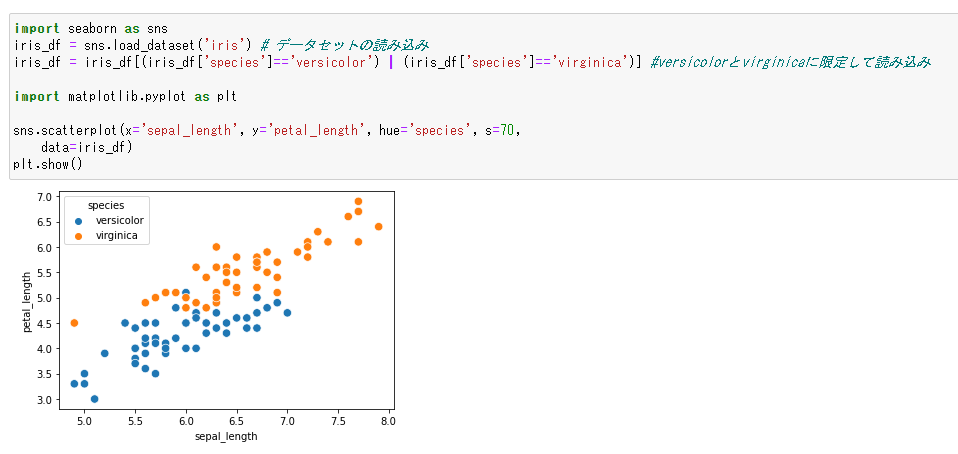
中間地点に線を引いてやれば、概ね分類することが出来ます。しかし、以下のようないびつなデータが存在した場合、どこに線を引いていいかわかりません。
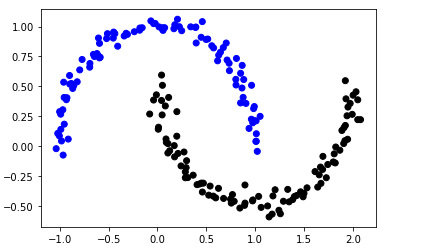
このようなデータを「線形分類不能」と呼び、サポートベクターマシンを適用することになります。
サポートベクターマシンを使う処理の流れ
それでは処理の流れをご説明します!
いびつなデータセットをscikit-learnを使って生成する
先程ご紹介したようないびつなデータセットはなかなか都合よく転がっていないので、scikit-learnを使って生成しましょう。make_moonという関数を使って生成します。
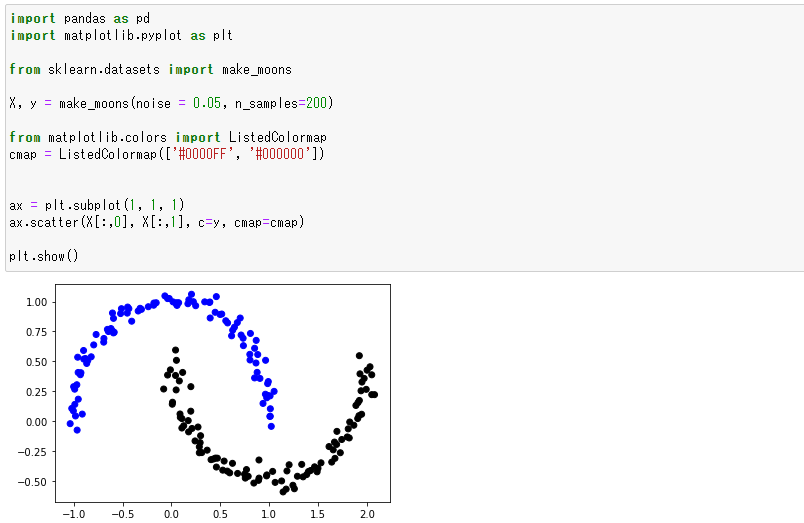
ロジスティクス回帰を使って分類してみる
比較のためにロジスティクス回帰を使って分類してみましょう。このコードは前回の記事とほぼ同じですので詳細な解説は割愛いたします。

以外にも0.8500のスコアが出てしまっていますが、三日月が重なる部分がそれほど多くないことが理由かと思います。
サポートベクターマシンを使って分類してみると…
それではサポートベクターマシンで分類をしてみましょう!scikit-learnからSVC(サポートベクターマシン)をインポートしてインスタンスを生成しています。引数として与えてある kernel=’rbf’ ですが、これはサポートベクターマシンのカーネル関数の一つです。なんなのか説明するにはえんえんと数式を書かねばならないので、詳細は割愛しますが、興味のある方はリンクよりご確認ください。

スコアは0.9900を記録し、かなりの高精度での分類が出来ていることを表しています!
サポートベクターマシンを使うサンプルコード
それではサンプルコードです!上記の処理の流れで分割したコードを以下に示します。
いびつなデータセットをscikit-learnを使って生成する
import pandas as pd import matplotlib.pyplot as plt from sklearn.datasets import make_moons X, y = make_moons(noise = 0.05, n_samples=200) from matplotlib.colors import ListedColormap cmap = ListedColormap(['#0000FF', '#000000']) ax = plt.subplot(1, 1, 1) ax.scatter(X[:,0], X[:,1], c=y, cmap=cmap) plt.show()
ロジスティクス回帰を使って分類してみる
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression
x_train, x_test, y_train, y_test = train_test_split(X, y,test_size=0.5)
algorithm = LogisticRegression()
algorithm.fit(x_train, y_train)
y_pred = algorithm.predict(x_test)
score = algorithm.score(x_test, y_test)
print(f'score: {score:.04f}')
サポートベクターマシンを使って分類してみると…
from sklearn.model_selection import train_test_split
from sklearn.svm import SVC
x_train, x_test, y_train, y_test = train_test_split(X, y,test_size=0.5)
algorithm = SVC(kernel='rbf')
algorithm.fit(x_train,y_train) # 学習
y_pred = algorithm.predict(x_test)
score = algorithm.score(x_test, y_test)
print(f'score: {score:.04f}')
おわりに
本記事では線形分類不能なデータをサポートベクターマシンで分類することにチャレンジしてみました。サポートベクターマシン自体は高度な数学的な理論が必要になりますので解説を割愛しましたが、scikit-learnから使う分にはカンタンだったのではないでしょうか?
実際のデータ分析では、分類が必要なデータで、カンタンに線形分類できるケースは稀だと思います。そのため、scikit-learnにはサポートベクターマシンを始めとしたたくさんのアルゴリズムが用意されています。我々としてはそのアルゴリズムを完全に理解しておく必要はありませんが、使う場合や使い方に関しては十分な知識を持っておきたいものです。
ただでこれだけ使えるものがあるのに、知らないというだけで使えないのはとてももったいないと私は思います笑